Answer:
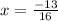
Explanation:
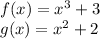
At the point of intersection, f(x)=g(x)
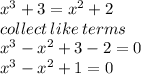
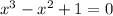
The above graph is that of the equation
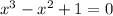
The solution is = -0.755 which is approximately -0.8
From the option provided;
For option A, x = -13/16 = -0.8125
For option B, x = -5/4 = -1.25
For option C, x = -15/16 = -0.9375
For option D, x = -7/8 = -0.875
From the option provided, The closest to the solution is Option A
Because - 0.8125 is approximately -0.8