I assume you're trying to simplify these.
For all of these, divide the coefficients separately from the x's and that separately from the y's.
#5:
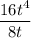
Start with 16/8 = 2.
Then move to
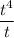 .
.
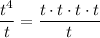
So, you'll cancel out one t from the top with the one t in the bottom and be left with
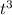 .
.
Putting that all together:
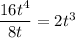
#6:
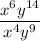
You have 6 x's in the top and 4 x's in the bottom. When you cancel out 4 from the top to cancel the 4 in the bottom, you'll be left with 2 x's in the top:
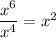
Similarly, 14 y's up top and 9 in the bottom. When you cancel one-for-one, you'll be left with 5 y's up top:
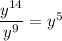
Putting that all together:
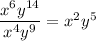
#7:
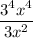
This is the same as #6, just with 3's and x's.
You have four 3's up top and one in the bottom. When you cancel, you'll be left with three 3's up top:
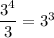
You have 4 x's up top and 2 x's down below. That will leave 2 x's up top once you cancel them out:
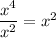
Putting that together:
