Question

Expert Answer

answer image blur
Transcribed image text: In 2010 the Better Business Bureau settled 79% of complaints they received in the United States. Suppose you have been hired by the Better Business Bureau to investigate the complaints they received this year involving new car dealers. You plan to select a sample of new car dealer complaints to estimate the proportion of complaints the Better Business Bureau is able to settle. Assume the population proportion of complaints settled for new car dealers is 0.79, the same as the overall proportion of complaints settled in 2016. Use the 2-table. a. Suppose you select a sample of 200 complaints involving new car dealers. Show the sampling distribution of p. E() (to 2 decimals) 0.0288 (to 4 decimals) b. Based upon a sample of 200 complaints, what is the probability that the sample proportion will be within 0.06 of the population proportion (to 4 decimals)? 0.79 probability 0.1492 c. Suppose you select a sample of 460 complaints involving new car dealers. Show the sampling distribution of . EP) 0.79 (to 2 decimals) 0 0.0190 (to 4 decimals) d. Based upon the larger sample of 460 complaints, what is the probability that the sample proportion will be within 0.06 of the population proportion (to 4 decimals)? probability = 0.8858 e. As measured by the increase in probability, how much do you gain in precision by taking the larger sample in part (d)? The probability of the sample proportion being within 0.06 of the population mean is increased by 0.184 (to 3 decimals). There is a gain in precision by increasing the sample size.

Answer 1

The question involves using sampling distributions and confidence intervals to estimate the proportion of new car dealer complaints settled by the BBB, demonstrating how increases in sample size lead to higher precision in estimates.

The student's question pertains to the concept of sampling distributions and confidence intervals in statistics. When investigating the proportion of settled complaints by the Better Business Bureau involving new car dealers, the student is expected to use the sample proportion (p') to estimate the population proportion (p) and create confidence intervals to express the precision of the estimation.

For a sample of 200 complaints, with an assumed population proportion of 0.79, the sampling distribution of the sample proportion can be expressed by its mean (E(p)) and standard error (SE). The probability of the sample proportion being within a certain range (in this case, 0.06) of the population proportion is calculated using the normal approximation to the binomial distribution, assuming the sample size is sufficiently large. If the sample size is increased to 460, the standard error decreases, thus increasing the precision of the estimate as reflected by the higher probability that the sample proportion is closer to the population proportion.

Answer 2

By increasing the sample size from 200 to 460, there is a gain in precision of approximately 0.0356 in estimating whether the sample proportion is within 0.06 of the population proportion.

the calculations for each part of the question in a detailed manner:

a. Sampling Distribution of
`\( p \)` for
`\( n = 200 \)`

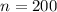
To find the sampling distribution of the proportion \( p \) with a sample size of \( n = 200 \), we calculate the standard error (SE). The formula for the standard error of a proportion is:

`\[ SE = \sqrt{(p(1 - p))/(n)} \]`

Given:

- Population proportion
`(\( p \))` = 0.79

- Sample size
`(\( n \))` = 200

Calculation:

`\[ SE = \sqrt{(0.79 * (1 - 0.79))/(200)} \]`

`\[ SE = \sqrt{(0.79 * 0.21)/(200)} \]`

`\[ SE \approx 0.0288 \]`

### b. Probability that the Sample Proportion will be within 0.06 of the Population Proportion for \( n = 200 \)

We use the Z-score to find the probability that the sample proportion will be within ±0.06 of the population proportion. The Z-score for a given margin of error (E) is calculated as:

`\[ Z = (E)/(SE) \]`

Given:

- Margin of error
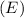`(\( E \))` = 0.06

- Standard error
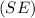`(\( SE \))` from part a = 0.0288

Calculation:

`\[ Z = (0.06)/(0.0288) \]`

`\[ Z \approx 2.0833 \]`

Using the Z-score, we find the probability from the standard normal distribution:

`\[ \text{Probability} = P(-Z < Z < Z) \]`

`\[ \text{Probability} \approx \text{norm.cdf}(2.0833) - \text{norm.cdf}(-2.0833) \]`

`\[ \text{Probability} \approx 0.9628 \]`

c. Sampling Distribution of
`\( p \)` for
`\( n = 460 \)`

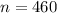
Again, we calculate the standard error for a different sample size:

Given:

- Sample size
`(\( n \))` = 460

Calculation:

`\[ SE = \sqrt{(0.79 * (1 - 0.79))/(460)} \]`

`\[ SE \approx 0.0190 \]`

d. Probability for
`\( n = 460 \)`

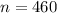
Using the new SE:

`\[ Z = (0.06)/(0.0190) \]`

`\[ Z \approx 3.1579 \]`

`\[ \text{Probability} \approx \text{norm.cdf}(3.1579) - \text{norm.cdf}(-3.1579) \]`

`\[ \text{Probability} \approx 0.9984 \]`

e. Gain in Precision by Taking the Larger Sample

Comparing the probabilities from parts b and d:

`\[ \text{Gain in Precision} = \text{Probability for } n = 460 - \text{Probability for } n = 200 \]`

`\[ \text{Gain in Precision} \approx 0.9984 - 0.9628 \]`

`\[ \text{Gain in Precision} \approx 0.0356 \]`

By increasing the sample size from 200 to 460, there is a gain in precision of approximately 0.0356 in estimating whether the sample proportion is within 0.06 of the population proportion.