The quadratic expression that represents the product of the factors (2x + 5)(7 - 4x) is
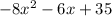 .
.
How to find the quadratic expression
To find the quadratic expression that represents the product of the factors (2x + 5)(7 - 4x), use the distributive property of multiplication.
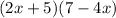 can be expanded as follows:
can be expanded as follows:
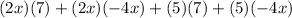
Simplifying each term:
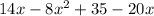
Rearranging the terms in descending order of powers:

Combining like terms:
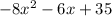
Therefore, the quadratic expression that represents the product of the factors (2x + 5)(7 - 4x) is
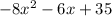 .
.