Question

For the following exercises, use shells to find the volumes of the given solids. Note that the rotated regions lie between the curve and the x-axis and are rotated around the y-axis. y=1−x² ,x=0, and x=1

Answer 1

To find the volume of the solid, we can use the method of shells.

Step-by-step explanation:

To find the volume of the solid, we can use the method of shells. Shells are cylindrical shells that are stacked together to form the solid. The volume of each shell is given by the formula V = 2πrhΔx, where r is the radius, h is the height, and Δx is the thickness of each shell. We need to integrate this formula over the interval [0,1] to find the total volume of the solid between the curve and the x-axis.

First, we need to find the radius of each shell. Since the solid is rotated around the y-axis, the distance between the y-axis and the curve y = 1-x^2 is equal to the radius of the shell. So, the radius is r = 1-x^2.

Next, we need to find the height of each shell. The height is equal to the difference between the upper and lower boundaries of the shell, which is given by h = x. Finally, we need to find the thickness of each shell. Since the solid is rotated around the y-axis, the thickness is equal to the difference between consecutive x-values, which is Δx = dx. Now, we can integrate the formula V = 2πrhΔx over the interval [0,1] to find the total volume of the solid.

Answer 2

The volumes of the given solids equivalent to
`$(\pi)/(2)$` cubic units

To find the volume of a solid generated by rotating the region bounded by the curve
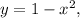`\( y = 1 - x^2 \),` the x-axis, and the vertical lines x = 0 and x = 1 around the y-axis, we can use the method of cylindrical shells. The volume of the solid is calculated by integrating the volume of infinitesimally thin cylindrical shells.

Step 1: Set Up the Integral

The volume of a typical shell is given by the formula:

`\[ V_{\text{shell}} = 2\pi rh \, dx \]`

where r is the radius of the shell (distance from the y-axis), h is the height of the shell, and dx is the thickness of the shell.

In this case:

- The radius of a shell at a point x is r = x .

- The height of the shell is given by the function
`\( y = 1 - x^2 \).`

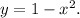
So, the volume of a shell is:

`\[ V_{\text{shell}} = 2\pi x(1 - x^2) \, dx \]`

Step 2: Integrate from 0 to 1

The total volume is obtained by integrating the volume of these shells from x = 0 to x = 1 :

`\[ V = \int_(0)^(1) 2\pi x(1 - x^2) \, dx \]`

Step 3: Calculate the Volume

Let's calculate the integral to find the volume.

The volume of the solid generated by rotating the region bounded by the curve
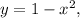`\( y = 1 - x^2 \),` the x-axis, and the vertical lines x = 0 and x = 1 around the y-axis is approximately 1.571 cubic units. This is equivalent to
`$(\pi)/(2)$` cubic units