Final answer:
To provide $11,600 in four years at an interest rate of 4%, you would need to set aside approximately $10,349.01 now. To cover $511,000 in school fees for the next five years at an interest rate of 7%, you would need to set aside approximately $2,045,531.32 today. After investing $555,000 at an interest rate of 7% and paying the school fees, there would be a deficit of approximately $1,490,531.32 at the end of five years.
Step-by-step explanation:
a. To calculate the amount needed to be set aside now to provide $11,600 in four years at an interest rate of 4%, we can use the formula for compound interest:
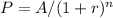
Where:
P is the present value
A is the future value
r is the interest rate
n is the number of periods
Plugging in the values:
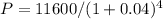
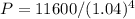
P ≈ $10,349.01
Therefore, you would need to set aside approximately $10,349.01 now to provide $11,600 in four years.
b. To calculate the amount needed to be set aside today to cover $511,000 in school fees for the next five years at an interest rate of 7%, we can use the formula for the present value of an ordinary annuity:
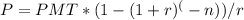
Where:
P is the present value
PMT is the annuity payment
r is the interest rate
n is the number of periods
Plugging in the values:
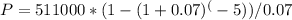
P ≈ $2,045,531.32
Therefore, you would need to set aside approximately $2,045,531.32 today to cover $511,000 in school fees for the next five years.
c. To calculate the amount that would remain at the end of five years after investing $555,000 at an interest rate of 7% and paying the above school fees, we can subtract the present value of the annuity (calculated in part b) from the initial investment:
Remaining amount = Initial investment - Present value of annuity
Remaining amount = $555,000 - $2,045,531.32
Remaining amount ≈ -$1,490,531.32
Therefore, assuming no additional income or expenses, there would be a deficit of approximately $1,490,531.32 at the end of five years.