After 17 years of compounding interest at 12% annually, your initial investment of $8,000 will grow to roughly $54,928.
To find the accumulated value of an investment of $8,000 at 12% compounded annually for 17 years, we can use the compound interest formula:
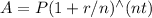
where:
A is the accumulated value
P is the principal amount (initial investment)
r is the annual interest rate
n is the number of compounding periods per year (in this case, 1 since it's compounded annually)
t is the total number of years
In this case:
P = $8,000
r = 12% (converted to decimal: 0.12)
n = 1
t = 17
Plugging these values into the formula, we get:
A = $8,000 (1 + 0.12/1) ^ (1 * 17)
A ≈ $54,928.33
Therefore, the accumulated value of the investment after 17 years is approximately $54,928.33.