Final answer:
The amount that results from the investment is $23,628.03.
Step-by-step explanation:
To find the amount that results from the investment, we can use the formula for compound interest.
The formula is given by
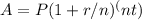
where A is the final amount, P is the initial principal, r is the annual interest rate, n is the number of compounding periods per year, and t is the time in years.
In this case, P = $14,000, r = 8% = 0.08, n = 2 (since it is compounded semiannually), and t = 5 years.
Plugging in these values into the formula, we get
A =
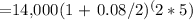
= $23,628.03.
Therefore, the amount that results from the investment is $23,628.03.