Question

Let f(x)={(mx-14 if x<-8),(x²+5x-6 if x>=-8):} If f(x) is a function which is continuous everywhere, then we must have m

Answer 1

Answer: -4

Explanation:

Let's imagine a graph of f(x) = x^2 + 5x - 6, x >= -8

We know that in the given range, this function is always continuous as it is a well-known form of quadratic function.

mx - 14 is also a continuous function in the given range, as it is a well known form of linear function.

So the only point where we are concerned with is at x = -8, in which the two continuous functions(Only in the given range) meet and should form a continuous function.

Here, let's go over the definition of continuous function:

It is a continuous function when a function f(x) for real number a satisfies the following limits

`\lim_(x \to \ a+) f(x) = \lim_(x \to \ a-) f(x) = f(a)`

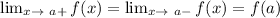
at every given point,

which basically just means that there shouldn't be any holes or jumps in the middle of a function.

In this case, we know that every other given points would be continuous except for the unknown point x =-8.

So let's connect them:

at x = -8,

`f(-8) = 18,\\\lim_(x \to \ 8+) f(x) = 18\\therefore,\\\lim_(x \to \ 8-) f(x) = 18`

as well in order for the function to satisfy as a continuous function.

Substituting,

m*(-8) - 14 = 18,

m = -4