Answer:
Perpendicular
Explanation:
To determine whether the given lines are parallel, perpendicular, or neither, we need to examine their slopes.

Recall the slope-intercept form of a line:
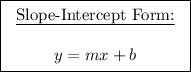
Where 'm' represents the slope of the line.
- If two lines have identical slopes, they run parallel to each other.
- When the slopes of the lines are negative reciprocals of one another, the lines are perpendicular.
- In cases where the slopes are neither equal nor negative reciprocals, the lines do not fit into the classifications of being parallel or perpendicular.

Our given lines:
y = 6x - 3
y = (-1/6)x + 7
Let's analyze the given lines:
The slopes of the lines can be determined by looking at the coefficients of the x terms.
For Line 1, the coefficient of the x term is 6, so its slope is 6.
For Line 2, the coefficient of the x term is -1/6, so its slope is -1/6.
These slopes are negative reciprocals of each other, thus these lines are perpendicular.

Additional Information:
Reciprocal: The reciprocal of a number is found by dividing 1 by that particular number. For any non-zero value 'a', its reciprocal 'b' is given by:
Negative Reciprocal: To derive the negative reciprocal of a number, first calculate its reciprocal, and then reverse the sign to make it negative. For a non-zero number 'a', the negative reciprocal 'c' is defined as: