Question

The range of the function f(x, y) = 4 - √4 - x² - y² is O [2,00) 0 (-00, 2] 0 (-00, 4 O (4,00) O [2, 4]

Answer 1

The range of the function f(x, y) = 4 - √4 - x² - y² is [2, 4].

Step-by-step explanation:

The given function is f(x, y) = 4 - √(4 - x² - y²). To find the range of this function, we need to determine the set of all possible values that the function can take. Since the square root of a number is always non-negative, the maximum value of the function occurs when the expression inside the square root is minimized. The minimum value of x² + y² is 0, when x and y are both 0. Substituting this into the function, we get f(0, 0) = 4 - √(4 - 0 - 0) = 4 - √4 = 4 - 2 = 2.

Therefore, the range of the given function is [2, 4].

Answer 2

The range of the function f(x, y) = 4 - √(4 - x² - y²) is [2, 4].

Step-by-step explanation:

The given function is
`f(x, y) = 4 - \sqrt{(4 - x^2 - y^2).`

To find the range of this function, we need to determine the possible values of f(x, y). Since the square root is only defined for non-negative numbers, the expression inside the square root must be greater than or equal to zero.

So, we have
`4 - x^2 - y^2 > 0.`

Rearranging this inequality, we get
`x^2 + y^2 < 4.`

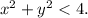
This represents a circle with radius 2 centered at the origin. The range of the function is the set of all possible values of f(x, y) for points within this circle.

Thus, the range of the function is [2,4].