Question

Find the value of x





A. 25
B. 35
C. 55
D. 10

Answer 1

Explanation:

c

Answer 2

`$$x = 7 \quad \text{or} \quad x = 1$$`

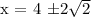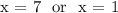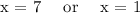
Let’s find the value of x in the equation:

`$$x^2-8x+7=0$$`

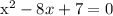
We can solve the equation using the quadratic formula, which is a general formula for solving quadratic equations.

Steps to solve:

1. Use the quadratic formula:

`\[ x = (-b \pm √(b^2 - 4ac))/(2a) \]`

where a, b, and c are the coefficients of the quadratic equation. In this case, a = 1, b = -8, and c = 7. Substituting these values into the formula, we get:

`\[ x = (-(-8) \pm √((-8)^2 - 4(1)(7)))/(2(1)) \]`

`\[ x = (8 \pm √(32))/(2) \]`

`\[ x = (8 \pm 4√(2))/(2) \]`

2. Separate the solutions and simplify:

`$$x = 4 \pm 2√(2)$$`

`$$x = 7 \text{ or } x = 1$$`