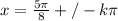Answer:
Explanation:
As far as the 2 asymptotes shown, here is how we would find them. Take the argument,
 , and set it equal to the parent asymptotes of
, and set it equal to the parent asymptotes of
 and
and
 and solve for x. These will give you the locations of the translated asymptotes.
and solve for x. These will give you the locations of the translated asymptotes.
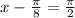 and
and
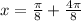 so
so
 . That's the vertical asymptote on the right. For the one on the left,
. That's the vertical asymptote on the right. For the one on the left,
 and
and
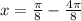 so
so
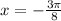 .
.
As far as the general solution goes,