Question

100 POINTS FOR THE FIRST CORRECT ANSWER! (Challenging Question)

A rectangle has length x and width y, where x and y are both positive integers. A uniform border is created around the rectangle by increasing both the length and width of the rectangle by 2 units. Given that the area of the border is equal to the area of the original rectangle, determine all possible dimensions for the rectangle.

Answer 1

Here’s my attempt. I used wolfram alpha to obtain the integer solutions at the end.

Answer 2

`x = 3, y = 10`

`x = 4, y = 6`

`x = 6, y = 4`

`x = 10, y = 3`

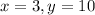
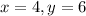
Explanation:

Given that a rectangle has length x and width y, and the area of any rectangle is the product of its length and width, then the area of the original rectangle is:

`\textsf{Area\;of\;original\;rectangle}=xy`

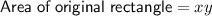
If a uniform border is created around the rectangle by increasing both the length and width of the rectangle by 2 units, then the area of the increased rectangle is:

`\textsf{Area\;of\;increased\;rectangle}=(x+2)(y+2)`

The area of the border is equal to the area of the increased rectangle minus the area of the original rectangle:

`\textsf{Area\;of\;border}=(x+2)(y+2)-xy`

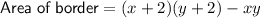
Given that the area of the border is equal to the area of the original rectangle, then:

`\begin{aligned}\textsf{Area of border}&=\textsf{Area of original rectangle}\\\\(x+2)(y+2)-xy&=xy\\\\xy+2x+2y+4-xy&=xy\\\\2x+2y+4&=xy\end{aligned}`

Rearrange the equation to isolate x:

`\begin{aligned}2x+2y+4&=xy\\\\2x-xy&=-2y-4\\\\x(2-y)&=-2y-4\\\\x&=(-2y-4)/(2-y)\\\\x&=(2(y+2))/(y-2)\end{aligned}`

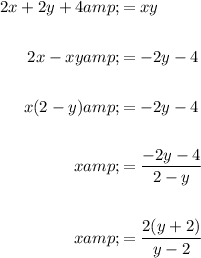
Rearrange the equation to isolate y:

`\begin{aligned}2x+2y+4&=xy\\\\2y-xy&=-2x-4\\\\y(2-x)&=-2x-4\\\\y&=(-2x-4)/(2-x)\\\\y&=(2(x+2))/(x-2)\end{aligned}`

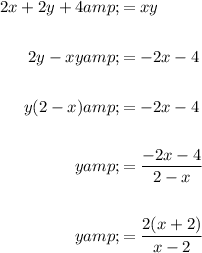
We can see that the equations for x and y are the same, but with the x and y variables swapped. Therefore, it doesn't matter which equation we use to find the positive integer solutions, so we will use the second equation where y is in terms of x.

`y=(2(x+2))/(x-2)`

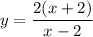
As the values of x and y are positive integers, then x ≥ 1 and y ≥ 1.

If the denominator of the equation is zero, the value of y is undefined. Therefore, x ≠ 2.

If 0 < x < 2, this would result in the value of y being negative.

Therefore, x must be greater than 2.

From inspection of the expression for y as a rational function, we can see that as x approaches +∞, y approaches 2 (from the positive side).

If x > 10 then y < 3. So any value of x that is bigger than 10 will result in a non-integer value of y between 2 and 3. Therefore, the values of x that will give a positive integer for y are in the interval 2 < x ≤ 10.

For y to always be an integer, the denominator must be a factor of the numerator. As we know that x is in the interval 2 < x ≤ 10, we can analyse the numerator and denominator (when x is an integer in the found interval) to determine which values of x will give a positive integer value of y.

If x = 3, the denominator is 1 and the numerator is 10. Since 1 is a factor of all integers, x = 3 is a valid value of x. The corresponding y-value is 10/1 = 10. This is also true if we swap the values: x = 10 and y = 3.

Therefore, x = 3 and y = 10, or x = 10 and y = 3, are possible dimensions for the rectangle.

If x = 4, the denominator is 2 and the numerator is 12. Since 2 is a factor of 12, x = 4 is a valid value of x. The corresponding y-value is 12/2 = 6.

This is also true if we swap the values: x = 6 and y = 4.

Therefore, x = 4 and y = 6 , or x = 6 and y = 4, are possible dimensions for the rectangle.

If x = 5, the denominator is 3 and the numerator is 14. Since 3 is not a factor of 14, x = 5 is a not a valid value of x.

We have already determined that x = 6 is a valid value of x.

If x = 7, the denominator is 5 and the numerator is 18. Since 5 is not a factor of 18, x = 7 is a not a valid value of x.

If x = 8, the denominator is 6 and the numerator is 20. Since 6 is not a factor of 20, x = 8 is a not a valid value of x.

If x = 9, the denominator is 7 and the numerator is 22. Since 7 is not a factor of 22, x = 9 is a not a valid value of x.

We have already determined that x = 10 is a valid value of x.

Therefore, all possible dimensions for the rectangle are:

• 
  `x = 3, y = 10`
• 
  `x = 4, y = 6`
• 
  `x = 6, y = 4`
• 
  `x = 10, y = 3`