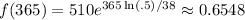Question

the half-life of chromium-51 is 38 days. If the sample contained 510 grams. How much would remain after 1 year?​

Answer 1

About 0.6548 grams will be remaining.

Explanation:

We can write an exponential function to model the situation. The standard exponential function is:

`f(t)=a(r)^t`

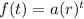
The original sample contained 510 grams. So, a = 510.

Each half-life, the amount decreases by half. So, r = 1/2.

For t, since one half-life occurs every 38 days, we can substitute t/38 for t, where t is the time in days.

Therefore, our function is:

`\displaystyle f(t)=510\Big((1)/(2)\Big)^(t/38)`

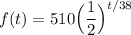
One year has 365 days.

Therefore, the amount remaining after one year will be:

`\displaystyle f(365)=510\Big((1)/(2)\Big)^(365/38)\approx0.6548`

About 0.6548 grams will be remaining.

Alternatively, we can use the standard exponential growth/decay function modeled by:

`f(t)=Ce^(kt)`

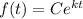
The starting sample is 510. So, C = 510.

After one half-life (38 days), the remaining amount will be 255. Therefore:

`255=510e^(38k)`

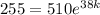
Solving for k:

`\displaystyle (1)/(2)=e^(38k)\Rightarrow k=(1)/(38)\ln\Big((1)/(2)\Big)`

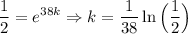
Thus, our function is:

`f(t)=510e^(t\ln(.5)/38)`

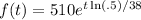
Then after one year or 365 days, the amount remaining will be about:

`f(365)=510e^(365\ln(.5)/38)\approx 0.6548`