Answer:
S₆ = 39060
Explanation:
the sum of a finite geometric sequence is
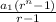
where a₁ is the first term and r the common ratio
the expression inside the ∑ is not in this form
so we require to find a₁ and r
the common ratio r =
 , then
, then
r =
 ← cancel 2 on numerator/ denominator
← cancel 2 on numerator/ denominator
=
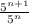
=
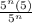 ← cancel
← cancel
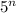 on numerator/ denominator
on numerator/ denominator
= 5
find first term in series a₁ by substituting in the lower bound and simplifying.
a₁ = 2
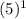 = 2 × 5 = 10
= 2 × 5 = 10
now substitute a₁ = 10 and r = 5 into the sum formula

=
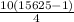
=
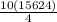
=

= 39060