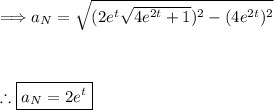Answer:
Q1:
![F(t) = m[6t \hat i + 12\hat j + 6t \hat k]](https://img.qammunity.org/2024/formulas/mathematics/college/ojq5aellaxhy731ba4vots0uxq5vnyx4i5.png)
Q2:
(a)
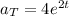
(b)
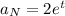
Explanation:
Q1: What force is required so that a particle of mass m has the position function r(t) = t³i + 6t² j + t³k?
To determine the force required for a particle with the given position function, we need to find the particle's acceleration first and then apply Newton's second law of motion.
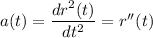
Taking the first derivative of r(t), we have:
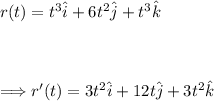
Now taking the second derivative:
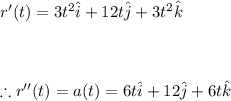
Now we can apply Newtons second law:
![\rightarrow F(t)=ma(t)\\\\\\\\\therefore \boxed{ F(t) = m[6t \hat i + 12\hat j + 6t \hat k]}](https://img.qammunity.org/2024/formulas/mathematics/college/vhvnzl02bnhb49lujkb093uhelftfnd556.png)

Q2: Find the tangential and normal components of the acceleration vector, r(t) = ti + 2eᵗj+e²ᵗk.
To find the tangential (a) and normal components (b) of the acceleration vector, we can use the following formulas:
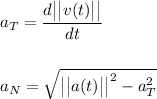
Part (a):
Finding v(t) by taking the derivative of r(t):
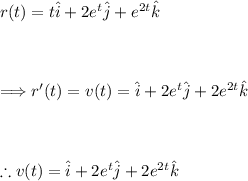
Find the magnitude of the velocity function using the following formula:
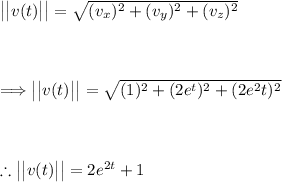
Now take the derivative of this function, we get:
![\Longrightarrow a_T=(d)/(dt)[2e^(2t)+1] \\\\\\\\\therefore \boxed{a_T=4e^(2t)}](https://img.qammunity.org/2024/formulas/mathematics/college/xx6x94u5mgopamo4ue6cd02uwvykot9qdp.png)
Part (b):
Start by finding a(t) by taking the derivative of v(t):

Now calculate the magnitude of a(t):
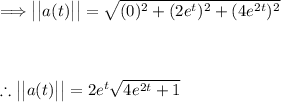
Substitute our expressions into the formula: