Answer:
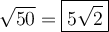
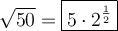
![\large\text{$\sqrt[10]{2^5}=\boxed{2^{(1)/(2)}}$}](https://img.qammunity.org/2024/formulas/mathematics/college/atdjl02w776chernu4brczq2ougox7mml0.png)
Explanation:
Given expression:
![\large\text{$\sqrt[10]{2^5}\cdot 5 \cdot 2^{-(1)/(2)}-\frac{√(50)}{2^{(1)/(2)}}$}](https://img.qammunity.org/2024/formulas/mathematics/college/as6o1yzmy3uaa3rxhn5px8fb358xlze3qu.png)
To simplify the given expression, begin by simplifying and rewriting the radicals.
To simplify the radical √(50) using perfect square factors, we can rewrite 50 as the product of 5² · 2:
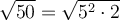

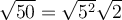
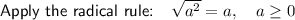
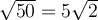
The square root can be represented as a rational exponent of 1/2. Therefore:

To rewrite
![\sqrt[10]{2^5}](https://img.qammunity.org/2024/formulas/mathematics/college/zygditofxj8zyj853mvwfzpvqk4crx9ycl.png) , we can apply the exponent rule
, we can apply the exponent rule
![\sqrt[n]{a^m}=a^{(m)/(n)}](https://img.qammunity.org/2024/formulas/mathematics/college/4sr2yzclqbw653b0m6oq6hon5pnjkwh5ls.png) :
:
![\large\text{$\sqrt[10]{2^5}=2^{(5)/(10)}=2^{(1)/(2)}$}](https://img.qammunity.org/2024/formulas/mathematics/college/h0o5z25iyvz9z7mun1jg9rcybnsbynplb2.png)
Therefore, the expression simplified by rewriting the radicals is:
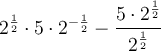
To simplify further, cancel the common factor
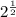 of the rational:
of the rational:
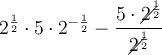
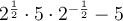

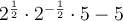
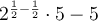
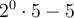
As any number to the power of zero is always 1:
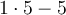
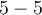
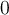
Therefore, the expression is equal to zero.