Answer: 2) 92.08
Explanation:
To find the perimeter, you need to use the distance formula which is
 .
.
To do this, you take 2 points, let's start with point M and point N. We have (13,-4) and (10,-10). Now, we have
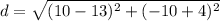 . From there, we get
. From there, we get
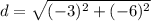 by doing addition and subtraction. After, we square both to get
by doing addition and subtraction. After, we square both to get
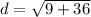 which is
which is
 which in decimal form is 6.7082039325 or 6.71 rounded to the nearest hundredth.
which in decimal form is 6.7082039325 or 6.71 rounded to the nearest hundredth.
Just like that, we can calculate the distance between the other 3 lines. Between points L and M, it's 33.94, between points L and K, it's 9,
and between points K and N, it's 42.43.
Now to find the perimeter, we add all those values up, and get 92.08 as our answer.
Hope that helped a lot.
:)