Question

Prove for all integers n, k, and r with n > and equal k > and equal r that ( n/k ) (k/r) = ( n/r) ( n-r/ n-r)

Answer 1

Definition:
An integer is a number that can be written without a fractional component. They can be positive, negative, or zero.

Explanation:

`\textsf{For the Question:}`

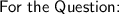
In order to prove that (n/k) * (k/r) = (n/r) * ((n-r)/(n-r)) for all integers n, k, and r with n ≥ k ≥ r, we can follow these steps:

• Simplify both sides of the equation.
• Use the fact that n ≥ k ≥ r to show that both sides are equal.

Let's proceed with the proof:

Simplify both sides of the equation.

Left-hand side (LHS):

(n/k) * (k/r)

Multiply the fractions:

LHS = (n * k) / (k * r) we can cancel out k.

LHS = n/r

Right-hand side (RHS):

(n/r) * ((n-r)/(n-r))

The (n-r) terms in the numerator and denominator of the RHS cancel out:

RHS = (n/r) * (1)

RHS = n/r

Use the fact that n ≥ k ≥ r to show that both sides are equal.

Since n ≥ k and k ≥ r, we can conclude that n ≥ r.

Thus, (n-r) is a non-negative integer, as (n-r) is the difference between two integers (n and r), and the result will always be an integer.

Hence Proved: