Answer:
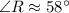
Explanation:
The Law of Cosines states that for any triangle ABC, where A, B, and C are angles and a, b, and c are sides:
 .
.
Since we wish to find R, we can use the law of cosines:
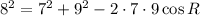
Solving for cos R, we find it to be 11/21. Taking the inverse cosine of this value, we find angle R to have a measure of 58.411864° ≈ 58°.