Answer:
25. x = 65, m∠TKR = 55°, m∠PKT = 85°
26. x = 50, m∠POL = 180°, m∠POK = 90°, m∠KOL = 90°
Explanation:
25.
We can see from the diagram that ∠PKR is made up of ∠TKR and ∠PKT. The question also tells us that m∠PKR = 140°. Therefore, we can set up the following equation and solve for x:
∠TKR + ∠PKT = ∠PKR
⇒
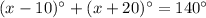
⇒
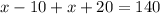 [Removing the brackets]
[Removing the brackets]
⇒
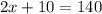 [Combining like terms]
[Combining like terms]
⇒
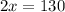 [Subtracting 10 from both sides of the equation]
[Subtracting 10 from both sides of the equation]
⇒
 [Dividing both sides by 2]
[Dividing both sides by 2]
⇒

Now that we have the value of x, we can simply substitute its value into the expressions for ∠TKR and ∠PKT to find their respective values:
m∠TKR = (x - 10)°
= (65 - 10)°
= 55°
m∠PKT = (x + 20)°
= (65 + 20)°
= 85°
26.
The question tells us that the line
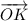 bisects ∠POL. This means the line
bisects ∠POL. This means the line
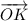 halves the angle POL. This means that ∠POK and ∠KOL are two halves of the angle POL. Therefore, we can set up the following formula and solve for x:
halves the angle POL. This means that ∠POK and ∠KOL are two halves of the angle POL. Therefore, we can set up the following formula and solve for x:
m∠POK =
 (∠POL)
(∠POL)
⇒
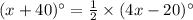
⇒
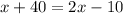
⇒
 [Subtracting 2x from both sides]
[Subtracting 2x from both sides]
⇒
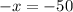
⇒

Therefore, we can find the values of ∠POL, ∠POK and ∠KOL using this value x:
m∠POL = (4x - 20)°
= (4 × 50 - 20)°
= (200 - 20)°
= 180°
m∠POK = (x + 40)°
= (50 + 40)°
= 90°
∠POK and ∠KOL are equal as they are halves of ∠POL. Therefore,
m∠KOL = m∠POK = 90°