Question

You are given the sample mean in the population standard deviation use this information to construct the 90% and 95% confidence intervals for the population mean interpret the results and compare the widths of confidence intervals from a random sample of 40 business days the main closing price of the certain stock was $116.11 assume the population standard deviation is $9.80

Answer 1

We are 90% confident that the interval from $113.56 to $118.66 captures the true mean closing price of the certain stock during business days.

We are 95% confident that the interval from $113.06 to $119.16 captures the true mean closing price of the certain stock during business days.

The 95% confidence interval is wider because as the confidence level increases, the width of the confidence interval increases (a larger interval increases the chance that the true value will be found in the interval).

Explanation:

I am assuming that the sample mean is $116.11, as that is the only given figure. If this is true, then we have that
`\bar{x}=116.11`,
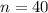`n=40`, and
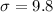`\sigma = 9.8`, where x-bar is the sample mean, n is the sample size, and sigma is the population standard deviation.

Because all three of the above statistics are know, we can use the given formula for a confidence interval:
`\bar{x} \ \pm \ z^* \ \cdot \ (\sigma)/(√(n))`, where z star is the critical value for a given confidence interval. It is important to note here that z-star is calculated using the normal curve, whereas the critical value t-star, which is used in finding the mean without knowing the population standard deviation, is found using a t-distribution.

We then find the z-star values for 90% confidence and 95% confidence using the invNorm function on a graphing calculator: z-star for 90% is approximately 1.64485, and z-star for 95% is approximately 1.96996.

We then plug these values into our formula:

For 90%:

`116.11 \pm 1.64485 \ \cdot \ (9.8)/(√(40)) \approx 116.11 \pm 2.55 = (113.56,118.66)`

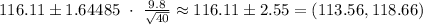
For 95%:

`116.11 \pm 1.96996 \ \cdot \ (9.8)/(√(40)) \approx 116.11 \pm 3.05 = (113.06,119.16)`

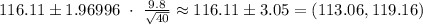
*Decimal places are rounded to the hundredths because units are in $