Final answer:
The value today of receiving $5,000 at the end of each six-month period for the next four years, assuming an annual interest rate of 4% compounded semi-annually, is $33,664.
Step-by-step explanation:
To calculate the value of a series of cash flows with compound interest, we use the formula:
![V = P[(1 + r/n)^(nt) - 1] / (r/n)](https://img.qammunity.org/2024/formulas/business/high-school/b2f4fg9fpwp8vvj40qws4471th0v8vsrni.png)
In this case, P is the present value (which is zero since we are finding the future value), r is the annual interest rate (4%), n is the number of times interest is compounded per year (2), and t is the number of years (4).
First, we calculate the future value of each $5,000 payment:
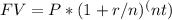
FV = 5,000*(1 + 0.02)^(2*4)
FV = $32,459 per payment
Next, we add up all the future values to get the total value:
V = FV1 + FV2 + FV3 + FV4
V = $32,459 * 4 = $129,836
However, we need to discount this amount back to today's value using the same formula:
![V = P[(1 + r/n)^(nt) - 1] / (r/n)V = 0[(1 + 0.02/2)^(2*4) - 1] / (0.02/2)](https://img.qammunity.org/2024/formulas/business/high-school/slizwmbm6woxak3wn6wi4wu2htys6ihuz6.png)
V = $33,664.09 (rounded to two decimal places)
Therefore, the total value today of receiving $5,000 at the end of each six-month period for the next four years with an annual interest rate of 4% compounded semi-annually is $33,664.