If a graph directs in the same direction(upward or downward), it's of an even degree, and vice versa. If it increases, it has a positive sign in the leading term, and the opposite is true.
3 of 6: even; negative
5 of 6: odd; negative
6 of 6: odd; positive
Principle
But you might want to see how it works, don't you? Let's see it, the limits!
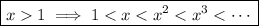
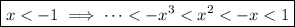
If the function heads toward the right infinity, it keeps the same direction. Okay, this is easy to understand, but what about another one? The sign alternates. The odd degree makes a turn!
What if the coefficient is significantly larger than the previous one?
Let's consider the coefficient. Since
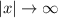 , no matter how greater the coefficient, its absolute value will be less than
, no matter how greater the coefficient, its absolute value will be less than
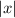 , which keeps the priority of the increment behind, so nothing matters!
, which keeps the priority of the increment behind, so nothing matters!