Question

The perimeter of the rectangle below is 88 units. Find the length of side WX.

Write your answer without variables.
4
V
4x
X
3x + 2
W

Answer 1

20 units

Explanation:

L = Length of rectangle = Side VW

= Side YX

=
`4x` units

W = Width of rectangle = Side WX

= Side VY

=
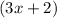`(3x + 2)` units

Perimeter of rectangle = 88 units

Perimeter of rectangle = Sum of exterior sides

=
`2(L + W)` units

`88 = 2[(4x) + (3x + 2)]`

`88 = 2[4x + 3x + 2]`

`88 = 2[7x + 2]`

`88 = 14x + 4`

`88 - 4 = 14x`

`14x = 84`

`x = (84)/(14)`

`x = 6`

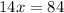
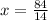
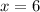
Substituting the calculated value of ‘x’ in the expression for the width of the rectangle:

Length of Side WX =
`[3(6) + 2]` units

=
`(18 + 2)` units

= 20 units