Question

Consider the following exponential probability density function. f(x)= 4

1
​
e − 4
x
​
for x≥0 a. Which of the following is the formula for P(x≤x 0
​
) ? 1P(x≤x 0
​
)=e − 4
x 0
​
​
2P(x≤x 0
​
)=1−e − 4
x 0
​
​
3P(x≤x 0
​
)=1−e −x 0
​
b. Find P(x≤1) (to 4 decimals). c. Find P(x≥3) (to 4 decimals). d. Find P(x≤6) (to 4 decimals). (3 e. Find P(1≤x≤6) (to 4 decimals)

Answer 1

Given the exponential probability density function,

A. P(X ≤ x₀) = 1 -
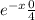`e^(-x)(0)/(4)`. Option 2

B. P(X ≤ 1) = 0.2212 C. P(x ≥ 3) = 0.4724
D. P(X ≤ 6) = 0.7769 E. P(1 ≤ x ≤ 6) = 0.5557

Explanation:

For the exponential probability density function
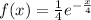`f(x) = (1)/(4) e^{-(x)/(4)` for x ≥ 0

A. The CDF of an exponential distribution is:

P (X ≤ x₀) =
`1 - e^(- \Lambda x_0)`

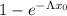
In this case, λ = 1/4. So the CDF is:

P(X ≤ x₀) =
`1 - e^{-x_(0)/(4)`

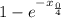
​The formula for P(X ≤ x₀) is ∴ P(X ≤ x₀) = 1 -
`e^(-x)(0)/(4)`.

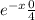B. To find P(X≤1) :

P(X ≤ 1) = 1 − e^[-1/4}

P(X ≤ 1) = 1−e^{−0.25}

P(X ≤ 1) = 1 − 0.7788 = 0.2212

C. To find P(X≥3), we use the complement rule:

P(X ≥ 3) = 1 − P(X ≤ 3)

P(X ≥ 3) = 1 − (1 − e^{−3/4})

P( X ≥ 3) = 1 − (1 − e^{−0.75})

P(X ≥ 3) = e^{−0.75} = 0.4724

D. To find P(X ≤ 6):

P(X ≤ 6) = 1−e^{−6/4}

P(X ≤ 6) = 1−e^{−1.5}

P(X ≤ 6) = 1 − 0.2231 = 0.7769

E. To find P(1 ≤ X ≤ 6):

P(1 ≤ X ≤ 6) = P(X ≤ 6) − P(X ≤ 1)

P(1 ≤ X ≤6) = 0.7769 − 0.2212 = 0.5557