Answer:
1) 135°
2) 133
3) 72
Explanation:
Question 1
To determine the interior angle of a regular polygon, we can use the formula:
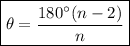
where:
- θ is the interior angle.
- n is the number of sides.
Given the number of sides of a regular octagon is 8, substitute n = 8 into the formula:

Therefore, the angle is 135°.

Question 2
The given diagram shows an isosceles trapezoid, since its legs are equal in length.
Opposite angles in an isosceles trapezoid are supplementary (sum to 180°). Therefore:
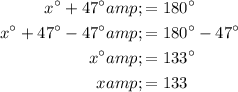
Therefore, the value of x is 133.

Question 3
The given diagram shows an isosceles trapezoid, since its legs are equal in length.
Opposite angles in an isosceles trapezoid are supplementary (sum to 180°). Therefore:
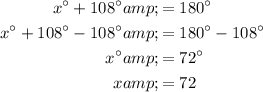
Therefore, the value of x is 72.