Answer:
x = 12.1
x = 3
Explanation:
From observation of the given right triangles, we can see that their interior angles are 30°, 60° and 90°. Therefore, they are special 30-60-90 triangles.
The side lengths in a 30-60-90 triangle have a special relationship which can be represented by the ratio 1 : √3 : 2.
The formula for the side lengths is a : a√3 : 2a, where "a" represents a scaling factor that can be any positive real number.
- Side a is opposite the 30° angle (shortest leg).
- Side a√3 is opposite the 60° angle (longest leg).
- Side 2a is the hypotenuse (longest side).
This ratio holds true regardless of the scale of the triangle. Therefore, if we know the length of one side of a 30-60-90 triangle, we can calculate the length of the other sides using this ratio.

In triangle one, the hypotenuse is c = 14. As 2a is the hypotenuse, we can use this to calculate the scale factor "a".
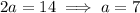
The side labelled "x" is opposite the 60° angle, and is therefore a√3. Therefore:
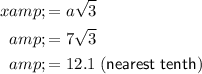
Therefore, the value of x is 12.1, rounded to the nearest tenth.

In triangle two, the hypotenuse is c = 6. As 2a is the hypotenuse, we can use this to calculate the scale factor "a".

The side labelled "x" is opposite the 30° angle, and is therefore simply "a". Therefore:
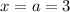
Therefore, the value of x is 3.
Note: Triangles 2 and 3 are the same.