The answer is:
24 ways
Work/explanation:
To find how many different ways the children can line up, we will find the factorial of 4 (because there are 4 children).
The factorial of 4 simply means we multiply it by itself, then the numbers that are less than 4 (these numbers are nonzero and non-negative).
The factorial is denoted as x!.
So now, we calculate the factorial of 4:
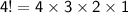
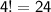
Hence, the answer is 24.