Answer: The zeroes of the function
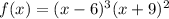 are
are
 and
and
 .
.
Explanation:
The zeroes of a polynomial are the x-values that make the polynomial equal to zero. For the given function
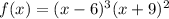 , the zeroes are the values of x that satisfy the equation
, the zeroes are the values of x that satisfy the equation
 .
.
Looking at the factors of the polynomial, we can see that the zeroes are:
-
 , because if we substitute
, because if we substitute
 into the function, we get
into the function, we get
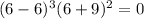 .
.
-
 , because if we substitute
, because if we substitute
 into the function, we get
into the function, we get
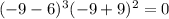 .
.
So, the zeroes of the function
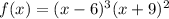 are
are
 and
and
 .
.