Question

Determining whether two functions are inverses of each other please help

Answer 1

see explanation

Explanation:

given f(x) and g(x)

if f(g(x)) = g(f(x)) = x

then f(x) and g(x) are inverses of each other

(a)

f(g(x))

= f(- 2x)

= -
`(-2x)/(2)` ( cancel 2 on numerator/ denominator )

= x

g(f(x))

= g(-
`(x)/(2)` )

= - 2 × -
`(x)/(2)` ( cancel 2 on numerator/ denominator )

= x

since f(g(x)) = g(f(x)) = x

then f(x) and g(x) are inverses of each other

(b)

f(g(x))

= f(
`(x-1)/(2)` )

= 2(
`(x-1)/(2)` ) + 1

= x - 1 + 1

= x

g(f(x))

= g(2x + 1)

=
`(2x+1-1)/(2)`

=
`(2x)/(2)`

= x

since f(g(x)) = g(f(x)) = x

then f(x) and g(x) are inverses of each other

Answer 2

`\begin{aligned} \textsf{(a)} \quad f(g(x))&=\boxed{x}\\g(f(x))&=\boxed{x}\end{aligned}\\\\\textsf{\;\;\;\;\;\;\;\;$f$ and $g$ are inverses of each other.}`

`\begin{aligned} \textsf{(b)} \quad f(g(x))&=\boxed{x}\\g(f(x))&=\boxed{x}\end{aligned}\\\\\textsf{\;\;\;\;\;\;\;\;$f$ and $g$ are inverses of each other.}`

Explanation:

Part (a)

Given functions:

`\begin{cases}f(x)=-(x)/(2)\\\\g(x)=-2x\end{cases}`

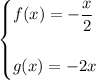
Evaluate the composite function f(g(x)):

`\begin{aligned}f(g(x))&=f(-2x)\\\\&=-(-2x)/(2)\\\\&=x\end{aligned}`

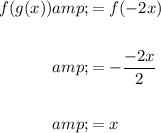
Evaluate the composite function g(f(x)):

`\begin{aligned}g(f(x))&=g\left(-(x)/(2)\right)\\\\&=-2\left(-(x)/(2)\right)\\\\&=x\end{aligned}`

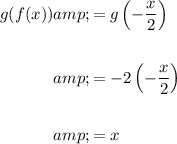
The definition of inverse functions states that two functions, f and g, are inverses of each other if and only if their compositions yield the identity function, i.e. f(g(x)) = g(f(x)) = x.

Therefore, as f(g(x)) = g(f(x)) = x, then f and g are inverses of each other.

`\hrulefill`

Part (b)

Given functions:

`\begin{cases}f(x)=2x+1\\\\g(x)=(x-1)/(2)\end{cases}`

Evaluate the composite function f(g(x)):

`\begin{aligned}f(g(x))&=f\left((x-1)/(2)\right)\\\\&=2\left((x-1)/(2)\right)+1\\\\&=(x-1)+1\\\\&=x\end{aligned}`

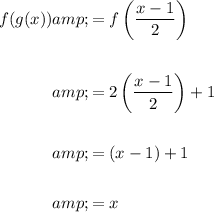
Evaluate the composite function g(f(x)):

`\begin{aligned}g(f(x))&=g(2x+1)\\\\&=((2x+1)-1)/(2)\\\\&=(2x)/(2)\\\\&=x\end{aligned}`

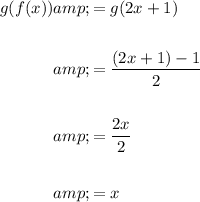
The definition of inverse functions states that two functions, f and g, are inverses of each other if and only if their compositions yield the identity function, i.e. f(g(x)) = g(f(x)) = x.

Therefore, as f(g(x)) = g(f(x)) = x, then f and g are inverses of each other.