Question

URGENT SOLVE TRIGONOMETRY

Answer 1

AB = 5.4

Explanation:

In a ΔPQR,

Law of sines :
`(sin(P))/(QR) = (sin(Q))/(PR)= (sin(R))/(PQ)`

Law of cosines:

`cos(P) = (PQ^2 + PR^2 - QR^2)/(2(PQ)(PR))\\\\cos(Q) = (PQ^2 + QR^2 - PR^2)/(2(PQ)(QR))\\\\cos(R) = (PR^2 + QR^2 - PQ^2)/(2(PR)(QR))`

In ΔCDE, by cosine law,

`cos(DCE) = (DC^2 + CE^2 - DE^2)/(2(DC)(CE))\\\\= (10^2 + 8^2 - 9^2)/(2(10)(8))\\\\= (100 + 64- 81)/(160)\\\\= (83)/(160)\\\\cos(DCE) = (83)/(160) \\\\\implies \angle DCE = cos^(-1)((83)/(160))\\\\\implies \angle DCE = 58.75`

In ΔABC, sine law,

`(sin(BAC))/(BC) =(sin(ABC))/(AC)=(sin(ACB))/(AB)\\\\\implies (sin(BAC))/(BC) =(sin(72))/(6)=(sin(ACB))/(AB)\\\\\implies (sin(72))/(6)=(sin(ACB))/(AB)\\\\\implies AB =(6sin(ACB))/(sin(72))\\\\`

∠DCE = ∠ACB (vertically opposite angles)

`\implies AB = (6sin(DCE))/(sin(72)) \\\\= (6*sin(58.75))/(sin(72)) \\\\= (6*0.85)/(0.95) \\\\= 5.4`

Answer 2

5.39 m

Explanation:

As line segments AE and BD intersect at point C, m∠ACB ≅ m∠ECD according to the vertical angles theorem.

As we have been given the lengths of all three sides of triangle DCE, we can use the Law of Cosines to find the measure of angle ECD, and thus the measure of angle ACB.

`\boxed{\begin{minipage}{6 cm}\underline{Cosine Rule} \\\\$c^2=a^2+b^2-2ab \cos C$\\\\where:\\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides.\\ \phantom{ww}$\bullet$ $C$ is the angle opposite side $c$. \\\end{minipage}}`

Given:

• a = CD = 10
• b = CE = 8
• c = DE = 9
• C = ∠ECD

Therefore:

`9^2=10^2+8^2-2(10)(8) \cos ECD`

`81=100+64-160 \cos ECD`

`81=164-160 \cos ECD`

`160 \cos ECD=164-81`

`160 \cos ECD=83`

`\cos ECD=(83)/(160)`

`m \angle ECD= \cos^(-1)\left((83)/(160)\right)`

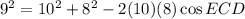
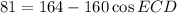
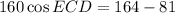
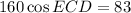
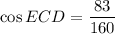
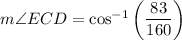
According to the vertical angles theorem, m∠ACB ≅ m∠ECD. Therefore:

`m \angle ACB= \cos^(-1)\left((83)/(160)\right)`

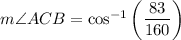
We now have two internal angles and one side length of triangle ACB:

`\bullet \quad m \angle ACB= \cos^(-1)\left((83)/(160)\right)`

`\bullet \quad m \angle ABC=72^(\circ)`

`\bullet \quad AC=6\; \sf m`

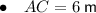
The distance between points A and B is the length of line segment AB.

To find this, we can use the Law of Sines.

`\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}`

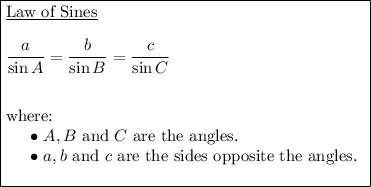
Substitute the values of AC, ∠ACB and ∠ABC into the formula and solve for AB:

`(AB)/(\sin \angle ACB)=(AC)/(\sin \angle ABC)`

`(AB)/(\sin \left(\cos^(-1)\left((83)/(160)\right)\right))=(6)/(\sin 72^(\circ))`

`(AB)/(\left((9√(231))/(160)\right))=(6)/(\sin 72^(\circ))`

`AB=(6)/(\sin 72^(\circ))\cdot \left((9√(231))/(160)\right)`

`AB=5.39353425...`

`AB=5.39\; \sf m\;(nearest\;hundredth)`

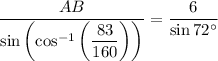
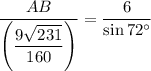
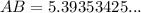
Therefore, posts A and B are 5.39 meters apart (rounded to the nearest hundredth of a meter).