Question

A verbal description of a function is given. To evaluate f(x), divide the input by 7 and add (6)/(7) to the result. (a) Find an algebraic representation for the function.

Answer 1

The algebraic representation of the function
`\(f(x)\)` is:

`\[f(x) = (x)/(3) + (2)/(3)\]`

To find an algebraic representation for the function
`\(f(x)\)` based on the verbal description, you need to perform two steps:

1. Divide the input by 3.

2. Add
`\((2)/(3)\)` to the result of the division.

Let's break this down step by step:

Step 1: Divide the input by 3.

To do this, you simply divide
`\(x\)` by 3. This can be represented as
`\((x)/(3)\)`.

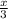Step 2: Add
`\((2)/(3)\)` to the result.

After dividing
`\(x\)` by 3, you add
`\((2)/(3)\)` to the result. So, you add
`\((2)/(3)\)` to
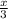`\((x)/(3)\)`. This can be represented as
`\((x)/(3) + (2)/(3)\)`.

Now, you can combine these two steps to obtain the algebraic representation of the function
`\(f(x)\)`:

`\[f(x) = (x)/(3) + (2)/(3)\]`

Answer 2

The algebraic representation of the verbal description "evaluate f(x), divide the input by 7 and add (6)/(7) to the result" is

`f(x) = ((x + 6))/(7)`

What is the algebraic representation of the function?

Let

the input be x

x divided by 7, then, add 6/7 to the result

`f(x) = (x)/(7) + (6)/(7)`

`f(x) = ((x + 6))/(7)`

Therefore,

`f(x) = ((x + 6))/(7)`