Let's denote the length of the shortest side as
 . Then, the other two sides would be
. Then, the other two sides would be
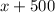 and
and
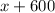 . Given that the perimeter of the lot is 2900 ft, we can set up the following equation:
. Given that the perimeter of the lot is 2900 ft, we can set up the following equation:
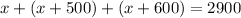
We can solve this equation to find the value of
 , and then use that value to find the lengths of the other two sides. Let's do that.
, and then use that value to find the lengths of the other two sides. Let's do that.
The solution to the equation is
 . This means that the shortest side of the triangle is 600 ft.
. This means that the shortest side of the triangle is 600 ft.
The other two sides can be found by adding 500 ft and 600 ft to the shortest side, respectively. Let's calculate these values.
The lengths of the sides of the lot are as follows:
- Shortest side: 600 ft
- Second side: 1100 ft (600 ft + 500 ft)
- Third side: 1200 ft (600 ft + 600 ft)
These lengths satisfy the condition that the perimeter of the lot is 2900 ft, as 600 ft + 1100 ft + 1200 ft = 2900 ft.