Answer:
B. -414,720 x⁷y⁶
Explanation:
To find the 4th term of the expansion of (2x - 3y²)¹⁰, we can use the binomial theorem.
The binomial theorem states that for an expression of the form (a + b)ⁿ:

For the expression (2x - 3y²)¹⁰:
Therefore, each term in the expression can be calculated using:

The 4th term is when r = 3. Therefore:
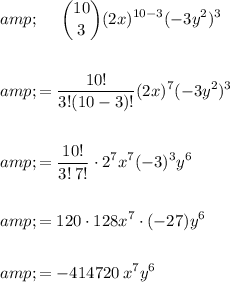
So the 4th term of the given expansion is:
