In
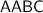 , it is given that:
, it is given that:
 ,
,
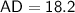 cm, and
cm, and
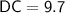 cm. We need to calculate the length of
cm. We need to calculate the length of
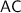 .
.
To solve this, we can use the Law of Cosines, which states:
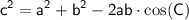
In our case, we have:

Substituting the given values:
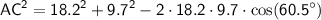
Now we can calculate
 :
:

Using a calculator or a mathematical software, we find that:
 cm
cm
Therefore, the length of
 is approximately
is approximately
 cm.
cm.