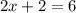Answer:
x = 2
Explanation:
First, we can rewrite all of the constants as exponential representations of 5.
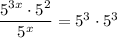
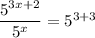
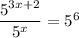
Next, we can take the log base 5 of both sides.
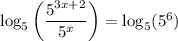

Then, we can apply the log quotient rule to the left side:
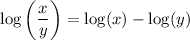
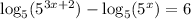
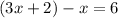
Finally, we can solve by combining like terms, then isolating x.