The answer is:
4 = k
Work/explanation:
Since we know the values of both x and y, we can plug them into the equation and solve for k:
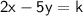

Simplify:

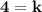
Therefore, k = 4.

Note : how do we know which number to plug in for x or y?
Well, if we remember the form of a point on the x-y plane, we'll know.
The form of the point is (x,y).
And here we have the point (2,0) where 2 = x and 0 = y.