To find the particular solution of the system
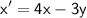 and
and
 that satisfies the initial conditions
that satisfies the initial conditions
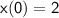 and
and
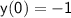 , we can use the method of solving a system of linear differential equations.
, we can use the method of solving a system of linear differential equations.
Let's first find the general solution of the system by solving the differential equations. We can rewrite the system in matrix form as follows:
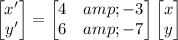 .
.
The coefficient matrix
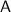 is
is
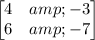 , and the vector
, and the vector
 is
is
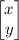 .
.
To find the general solution, we need to find the eigenvalues and eigenvectors of matrix
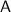 .
.
By solving
 , where
, where
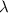 is the eigenvalue and
is the eigenvalue and
 is the identity matrix, we can find the eigenvalues.
is the identity matrix, we can find the eigenvalues.
Solving
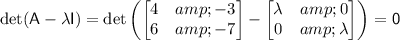 , we get
, we get
 .
.
Solving the quadratic equation, we find
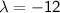 and
and
 .
.
Next, we find the corresponding eigenvectors by solving
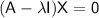 for each eigenvalue.
for each eigenvalue.
For
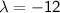 , we have
, we have
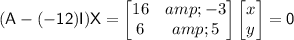 . By solving this system of equations, we find
. By solving this system of equations, we find
 .
.
For
 , we have
, we have
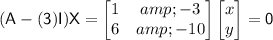 . By solving this system of equations, we find
. By solving this system of equations, we find
 .
.
The general solution of the system is given by
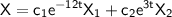 , where
, where
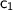 and
and
 are constants, and
are constants, and
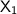 and
and
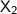 are the eigenvectors corresponding to the eigenvalues -12 and 3, respectively.
are the eigenvectors corresponding to the eigenvalues -12 and 3, respectively.
To find the particular solution that satisfies the initial conditions
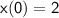 and
and
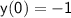 , we substitute these values into the general solution and solve for the constants
, we substitute these values into the general solution and solve for the constants
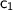 and
and
 .
.
Substituting
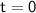 ,
,
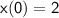 , and
, and
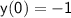 into the general solution, we have:
into the general solution, we have:
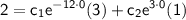 ,
,
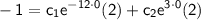 .
.
Simplifying these equations, we get:
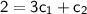 ,
,
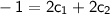 .
.
Solving this system of equations, we find
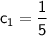 and
and
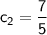 .
.
Therefore, the particular solution of the system that satisfies the initial conditions is:
 .
.