Answer:
The largest value of x + y = 26
Explanation:
Since ABCD is a square, all sides are equal so,
AB = BC = CD = DA = 26
AS = DQ = x
AR = BP = y
We first find all the sides, the inner figures are rectangles, so we can find the area by finding the sides,
First , we find the areas of the two black rectangles,
For rectangle ASRO (We define O as the point connecting the 4 rectangles)
We need to find AR and AS
Now, AR = y
And, AS = x
SO, we get the area,
Area of ASRO = (AR)(AS)
Area of ASRO = xy
For Rectangle PCQO
We see from figure that,
PC = BC - BP = 26 - y
PC = 26 - y
QC = DC - DQ
QC = 26 - x
So, the area will be,
Area of PCQO = (PC)(QC) = (26 - y)(26 - x)
Area of PCQO = 676 - 26x - 26y + xy
Now, we find the area of the light rectangles,
For Rectangle RDQO,
DQ = x
RD = DA - AR
RD = 26 - y
So,
Area of RDQO = (DQ)(RD) = x(26 - y)
Area of RDQO = 26x - xy
For rectangle SBPO,
BP = y
SB = AB - AS
SB = 26 - x
So,
Area of SBPO = (BP)(SB) = y(26 - x)
Area of SBPO = 26y - xy
Now, we have found all the areas and we are given that the sum of the areas of the light rectangles is equal to the sum of the areas of the dark rectangles (Area of black region is equal to area of white region), so,
Area of ASRO + Area of PCQO = Area of RDQO + Area of SBPO
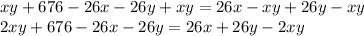
Taking everything to the right side,
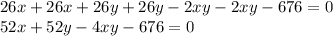
Dividing both sides by 4,
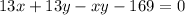
Now, we simplify,
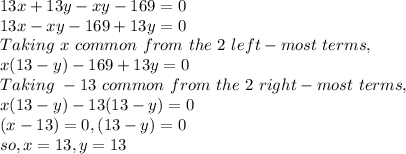
Hence the maximum value for x + y = 13 + 13 = 26