The answer is:
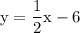
Work/explanation:
Given the slope and a point on the line, we can write the equation in point slope form, which is:
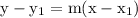
Where m is the slope and (x₁, y₁).
Plug the data in the formula:

Simplify:
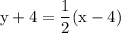
Now focus on the right side & simplify it :
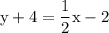
Finally, subtract 4 on each side:
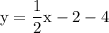
Simplify:
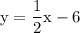
This is our equation in slope intercept form.
Therefore, the answer is y = 1/2x - 6.