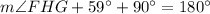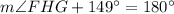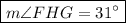Answer:

Explanation:
The inscribed angle in the given circle is ∠NLM.
The intercepted arc in the given circle is arc NM = 186°.
According to the Inscribed Angle Theorem, the measure of an inscribed angle is half the measure of the intercepted arc.
Therefore:

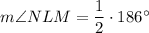
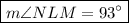

According to the Inscribed Angle Theorem, the measure of an inscribed angle is half the measure of the intercepted arc. Therefore:
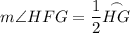

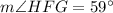
As line segment FH passes through the center of the circle, FH is the diameter of the circle. Since the angle at the circumference in a semicircle is a right angle, then:
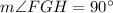
The interior angles of a triangle sum to 180°. Therefore: