

- Total number of students = 35
- Students present on Monday =
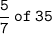


- Students not present on Monday = ?


As, we have :
Students present on Monday =
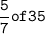

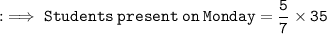
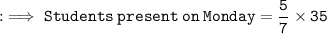

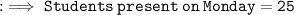

Now, we have to find students not present on Monday :
As, we have :
- Total number of students = 35
- Students present on Monday = 25

Therefore,
Students absent on Monday = 35 - 25 = 10

Hence, 10 students were not present on Monday.