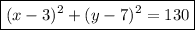Answer:
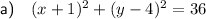
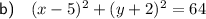
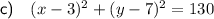
Explanation:
To write the equation of a circle given its center and radius, we can substitute the values into the standard circle equation formula.

Part a
Given values:
- Center (a, b) = (-1, 4)
- Radius r = 6
Substitute the values into the circle equation formula:
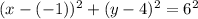
Therefore, the equation of the circle is:


Part b
Given values:
- Center (a, b) = (5, -2)
- Diameter = 16
The diameter of a circle is twice its radius.
Therefore, if the diameter of the circle is 16, the radius is r = 8.
Substitute the values into the circle equation formula:
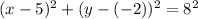
Therefore, the equation of the circle is:
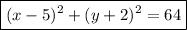

Part c
Given values:
- Center (a, b) = (3, 7)
- Point on the circle = (-4, -2)
Substitute the values into the circle equation formula and solve for r²:
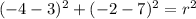
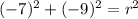
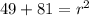
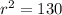
Therefore, the equation of the circle is: