Question

Question in the picture ​

Answer 1

2) Minimum = 15
Lower Quartile = 19
Median = 30.5
Upper Quartile = 45
Maximum = 62

3) Minimum = 82
Lower Quartile = 89
Median = 99.5
Upper Quartile = 112.5
Maximum = 120

Explanation:

A box and whisker plot (also known as a "box plot"), is a graph displaying the distribution of a set of data based on a five number summary.

Five-number summary

• Minimum: The minimum data value.
• Lower Quartile: The median of the data points to the left of the median.
• Median: The middle value when all data values are placed in order of size.
• Upper Quartile: The median of the data points to the right of the median.
• Maximum: The maximum data value.

`\hrulefill`

Question 2

Given data set:

• 45, 30, 22, 15, 18, 62, 19, 31, 50, 44

To calculate the values of the five-number summary, order the given data values from smallest to largest:

• 15, 18, 19, 22, 30, 31, 44, 45, 50, 62

There are 10 data values in the data set, so this is an even data set.

As there are an even number of data values, the median is the mean of the middle two values, 30 and 31:

`\sf Median=(30+31)/(2)=30.5`

The lower quartile is the median of the data points to the left of the median. Therefore:

• Lower Quartile = 19

The upper quartile is the median of the data points to the right of the median. Therefore:

• Upper Quartile = 45

Therefore, the five-number summary of the given data set is:

• Minimum = 15
• Lower Quartile = 19
• Median = 30.5
• Upper Quartile = 45
• Maximum = 62

To draw the box-and-whisker plot (see attachment 1):

• Label the ticks of the given number line from 5 to 65 in increments of 5.
• Draw a box from the lower quartile (19) to the upper quartile (45).
• Add the median (30.5) as a vertical line through the box.
• The whiskers are horizontal lines from each quartile to the minimum (15) and maximum values (62).

`\hrulefill`

Question 3

Given data set:

• 120, 108, 96, 82, 115, 88, 90, 120, 110, 99, 84, 100

To calculate the values of the five-number summary, order the given data values from smallest to largest:

• 82, 84, 88, 90, 96, 99, 100, 108, 110, 115, 120, 120

There are 12 data values in the data set, so this is an even data set.

As there are an even number of data values, the median is the mean of the middle two values, 99 and 100:

`\sf Median=(99+100)/(2)=99.5`

The lower quartile is the median of the data points to the left of the median. As there is an even number of data points to the left of the median, the lower quartile is the mean of the middle two values, 88 and 90:

`\sf Lower\;Quartile=(88+90)/(2)=89`

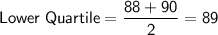
The upper quartile is the median of the data points to the right of the median. As there is an even number of data points to the right of the median, the upper quartile is the mean of the middle two values, 110 and 115:

`\sf Upper\;Quartile=(110+115)/(2)=112.5`

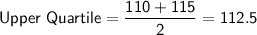
Therefore, the five-number summary of the given data set is:

• Minimum = 82
• Lower Quartile = 89
• Median = 99.5
• Upper Quartile = 112.5
• Maximum = 120

To draw the box-and-whisker plot (see attachment 2):

• Label the ticks of the given number line from 70 to 130 in increments of 5.
• Draw a box from the lower quartile (89) to the upper quartile (112.5).
• Add the median (99.5) as a vertical line through the box.
• The whiskers are horizontal lines from each quartile to the minimum (82) and maximum values (120).