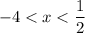Question

X+4
What is the solution of 2x-1 <0?
-45x5/1/2
0-4 0-45x2
-4

Answer 1

-4 < x < 1/2

Explanation:

Given the inequality:

`\displaystyle{(x+4)/(2x-1) < 0}`

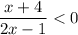
Where x can not equal 1/2 since it will result the undefined expression. Furthermore, by solving a rational inequality (fractional inequality) is different from solving a linear inequality.

If we assume that for the expression on the left side is always positive, we can say that:

`\displaystyle{(x+4)/(2x-1) < 0}`

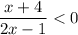
However, the expression can remain negative. If a denominator remains somewhat negative and you multiply both sides by the denominator, you'll end up from < to >, basically swap in inequality sign.

Thus. If we let x > 1/2, the interval where the expression is always positive, we can solve the inequality as:

`\displaystyle{(x+4)/(2x-1) \cdot \left(2x-1\right) < 0 \cdot \left(2x-1\right)}\\\\\displaystyle{x+4 < 0}\\\\\displaystyle{x < -4}`

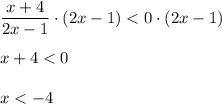
However, this inequality is false so we can say that there's no region where this expression is less than 0 at x > 1/2.

Now let's say that at x < 1/2, the expression will start to remain in negative (although there is an interval that the expression is positive at x < 1/2 but majority negative.) Therefore, let's say:

`\displaystyle{-(x+4)/(2x-1) < 0}\\\\\displaystyle{(x+4)/(2x-1) > 0}`

When we solve for the inequality, we should have x + 4 > 0 which results in x > -4. When union x > -4 with x < 1/2, it fits perfectly. Thus, the solution is:

`\displaystyle{-4 < x < (1)/(2)}`