The answer is:
1/4¹⁰
Work/explanation:
For this problem, I'm going to use the following exponent law:
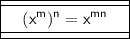
So if we have "a power to a power", we multiply the powers.
And now that we're familiar with this property let's apply it.
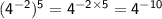
Here the next exponent law comes into play.
______________________
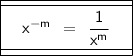
So if we have a number raised to a negative power, we flop it over.
Let's apply the law to our problem now.
Our problem is:
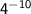
According to the law above, we should do the following:
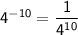
It's better to leave the answer as it is.
Hence, the answer is 1/4¹⁰