Question

NO LINKS!! URGENT HELP PLEASE!!

Problem 3: x =
Arc BD=

Answer 1

Answer: arcBD = 122

Explanation:

CB is the diameter line so that means that the angles on either side of the diameter = 180

Let's call the center O

<BOC + <DOC = 180 > Substitute

10x - 18 + 4x + 2 = 180 >Combine like terms

14x - 16 = 180 >Add 16 to both sides

14x = 196 >Divide both sides by 14

x = 14

<BOD = 10x -18

<BOD = 10(14) -18

<BOD = 140 -18

<BOD = 122

Because the <BOD starts at center the arc angle is the same as the angle

<BOD = arcBD

arcBD = 122

Answer 2

`x = 14`

`\overset{\frown}{BD}=122^(\circ)`

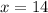
Explanation:

The given diagram shows a circle with diameter BC and radius OD (where O is the center of the circle).

Angles on a straight line sum to 180°. Therefore:

`(10x-18)^(\circ)+(4x+2)^(\circ)=180^(\circ)`

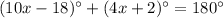
Solving the equation for x:

`(10x-18)^(\circ)+(4x+2)^(\circ)=180^(\circ)`

`10x-18+4x+2=180`

`14x-16=180`

`14x-16+16=180+16`

`14x=196`

`(14x)/(14)=(196)/(14)`

`x=14`

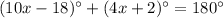
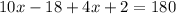
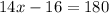
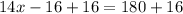
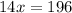
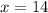
Therefore, the value of x is 14.

The measure of an arc is equal to the measure of its corresponding central angle.

To find the measure of arc BD, substitute the found value of x into the expression of the arc's corresponding central angle.

`\overset{\frown}{BD}=(10x-18)^(\circ)`

`\overset{\frown}{BD}=(10(14)-18)^(\circ)`

`\overset{\frown}{BD}=(140-18)^(\circ)`

`\overset{\frown}{BD}=122^(\circ)`

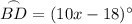
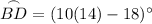
Therefore, the measure of arc BD is 122°.