Sin^2 150 de grade + sin^2 60 de grade =1

Question

asked Feb 12, 2024 49.9k views

1 Answer

Shmewnix · Answer 1 · 2024-02-18T14:13:41+0000

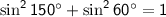
$\sf\sin^2 150^\circ + \sin^2 60^\circ = 1 \\$

Step 1: Convert degrees to radians:

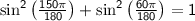
$\sf\sin^2 \left((150\pi)/(180)\right) + \sin^2 \left((60\pi)/(180)\right) = 1 \\$

Step 2: Simplify the expressions using the trigonometric identity:

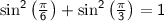
$\sf\sin^2 \left((\pi)/(6)\right) + \sin^2 \left((\pi)/(3)\right) = 1 \\$

Step 3: Recall the values of sine for angles
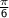$\sf (\pi)/(6) \\$ and
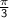$\sf (\pi)/(3) \\$ :

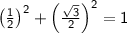
$\sf\left((1)/(2)\right)^2 + \left((√(3))/(2)\right)^2 = 1 \\$

Step 4: Evaluate the squares and simplify further:

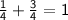
$\sf(1)/(4) + (3)/(4) = 1 \\$

Step 5: Combine the fractions:

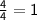
$\sf(4)/(4) = 1 \\$

Step 6: Simplify the fraction:

$\sf1 = 1 \\$

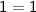
Thus, the equation
$\sf \sin^2 150^\circ + \sin^2 60^\circ = 1 \\$ is verified and true.